Problem

For the last year or so, I had become interested in anything to do with maps, countries, flags and physical geography. But when I looked at my globe, and then at my world map, I wondered how flat maps are made from a spherical world.That thought started this project. 

After quenching my curiosity online, I learned that there are different types of maps called projections. I also saw that there was a unique problem with all different map projections relating to how it is impossible to flatten a sphere. In fact,there are many projections that people can choose from, yet each projection has a separate problem. The two most common problems are size distortion, making land masses larger or smaller than they actually are depending on their position, or shape distortion, making a landmass' appearance incorrect.

Size distortion is a bad trait to have on a map if you are trying to compare what X country’s size is to Y country's size. For example the most common size distortion map is the Mercator projection which stretches out the edges making places like Greenland and Antarctica significantly bigger than they are supposed to be (See Figure 1). However with the Mercator projection, any direction (N,W,S,E,NW,...) is exactly that direction on the map, so it is very good for navigation.

Figure 1 : Mercator Projection. Notice the enlarged Greenland and Antarctica, as well as all the directions being well placed.🌍

Other map projections can have the sizes of landmasses exactly correct, allowing size comparisons to be accurate (See Figure 2), but these usually have shape distortion. But sadly, other parts of comparing are not so accurate, especially traits like width and shape, holding back the entire accuracy of the map. These distorted maps also let details in the maps disappear due to the crunching up of more northern, southern, and edge landmasses such as in the sinusoidal projection, but the more centered countries still have a more accurate shape.Other map projections similar to the Mercator projection can have extremely accurate shapes on the map, even if they are distorted in a different way.

 

Figure 2 : Sinusoidal Projection. Notice that the size is conserved, yet the shapes of the land masses are distorted.

There are many map projections, but each one has at least one problem, such as distorting the size or shape. In this project I attempted to solve these problems and find a way to flatten a globe to minimize distortion.

Problem: How to flatten a globe with minimal distortion? How to change a 3D surface to 2D surface?

 

Method

The following are three methods that I used to transform a 3D surface to a 2D surface.

Method One: Cutting a Beach Ball

Just a couple of months before I started science fair, I got an inflatable globe for my birthday, and this gave me an idea of how I would get my data. I would cut beach balls in a multitude of ways to flatten the sphere as much as possible. I bought several plastic, inflatable, beach balls, and then I prepared the balls by drawing the latitudes and longitudes  imitating a globe. I initially decided to cut all of the balls in the style of various sports balls because balls are stitched together with 2D surfaces to create a sphere: 

1. A beach ball, cut on the meridians. (Vertical lines that divide the colors).
2. A soccer ball pattern, with hexagons and pentagons.
3. A baseball/tennis ball, cuts a sphere into two equal area pieces.
4. A basketball, a baseball that was cut into quarters.
5. A volleyball, eighteen panels, that make six squares.

When thinking what other pattern I could use to flatten a sphere, I made:

6. A spiral pattern, kind of like an orange peel.
7. A spider type pattern, where I cut along a single meridian to cut a slit, and then cut along the parallels almost completely. 

I drew my patterns on the balls with a sharpie, and a long, bendy ruler to make the measurements as accurate as possible. I cut out those balls to make the flattest possible surface, but still keeping a good relationship between pieces of land (See Figure 3 for example).

Figure 3 : Latitudes and Longitudes. Notice how the image on the left is more bumpy than the image on the right, but it has more connections between the pieces.

Method Two: Projections

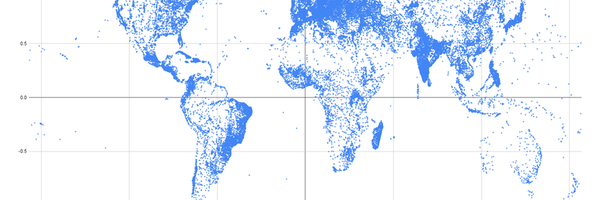
After researching about projections, I wanted to create some on my own.The first step was to find longitude and latitude data of the land masses on earth.This herculean task was fruitless, so instead I found the latitude and longitude of every city on earth. I inputted the data into google sheets and plotted the points.This worked just fine, and the scatter plot appeared as if it was the land masses themselves. Then, I searched up different projection equations to apply to the longitude and/or latitude. I applied:

1.  Gall Stereographic,
2.  Sinusoidal,
3.  Mercator,
4.  Lambert,
5.  Central Cylindrical,
6. Equirectangular

formulas to every city's coordinates, and saw how they changed the world’s appearance.

 While I could see how a unique projection changed the globe's appearance, I couldn’t tell exactly how the formulas changed the map. Therefore, instead of every city’s coordinates, I created a numerical grid on a scatter plot. After applying the projection formulas, I could really see every projection's distortion. (See Figure 4)

Figure 4 : Sinusoidal Trinity. Notice the top image is a sinusoidal grid, the middle image is using every city on earth, and the final image is a sinusoidal projection map.

 

Method Three: Lenses

In science class at school, I learned about lenses and mirrors, and how convex lenses can create a real image. During an experiment, we drew a picture on a light bulb, and shone it through a lens to create a larger image on a screen. I then took this idea and decided to apply it to creating a flat map.

 Initially I attempted to draw longitudes and latitudes on a spherical lightbulb, and shined it through a lens to magnify the pattern (See Figure 5). Trying to draw parallel and meridian patterns by hand proved inconsistent, thus, I made a circular stamp to apply a pattern to another light bulb, making the pattern much more consistent and able to be compared/ measured. I then used the same lens to magnify the stamped light bulb, and drew what was magnified onto a large piece of paper, comparing the size of the edge circles to the central circles.

Figure 5 : Magnified Bulb. Notice the lens and how large the magnified image is.

Research

• Projections

  • Types of Projections

    • What are they?
      • They distort the longitude and latitude coordinates onto a 2D plane.
    • Examples of famous projections are;  
      • Sinusoidal, equal area, and diamond-shaped,
      • Mercator, stretches the poles and shows the shapes very well,
      • Lambert, viewed from a pole and cut from a conical shape,
      • Central Cylindrical, over-stretches the poles,
      • Equirectangular, the poles are squished vertically but widened as well,
      • Gall Peters, stretches out the center area to show correct sizes but extremely distorts the shape. Ranking Projections
    • How much Size and Shape distortion?

  • How to Create Projections

    • On a globe, λ = Longitude, φ = Latitude, λ₀ = longitude of the central meridian, φ₀ = latitude of the central parallel.
    • On a map, x = →, y = ↑
    • Analyzed via area conservation, shape distortion, and orientation.

 

• Convex lenses

  • Convex lenses can create real images that are magnified, which you can project onto a piece of paper. If you use a sphere as the light source, you can almost make an orthographic projection. (A view of a sphere from infinitely far away.)

 

• How to Cut Different Ball Shapes

  • Beach Ball

    • Cut on the longitudes to make a flower shape.

  • Soccer Ball

    • Cut out of hexagons and pentagons.

  • Tennis Ball

    • Cut a sphere into two equal area sides that can be smoothened.

• Volleyball

  • Cut into 18 strips, 3 to make 6 equal area squares.

• Basketball

  • A tennis ball shape, cut into two.

Results

I got the following results from trying to transform a 3D surface into a 2D surface.

Results One: Cutting a Beach Ball

1. A beach ball, cut on the meridians. (Vertical lines that divide the colors).

 

2. A soccer ball pattern, with hexagons and pentagons.

 

3. A baseball/tennis ball, cuts a sphere into two equal area pieces.

 

4. A basketball, a baseball that was cut into quarters.

 

5. A volleyball, eighteen panels that make six squares.

 

When thinking about what other patterns I could use to flatten a sphere, I made:

6. A spiral pattern, kind of like an orange peel.

 

7. A spider-type pattern, where I cut along a single meridian to cut a slit, and then cut along the parallels almost completely. 

 

After cutting all the different patterns on beach balls, I then needed a way to rank them, to see which of the ball cuttings was the best strategy for a map. So, I took photographs of the patterns laid out on the floor from a bird's-eye view and painted the background(everything but the beach ball) green. I did this because that color did not show up anywhere in the patterns of the beach ball, and then I could use a computer graphics program (GIMP) to count the number of pixels of the photograph that were green. I then cropped the image two ways: 1. Connected Map: I created these maps as if one tightened a string around the edges, not allowing any concave areas of the map. 2. Efficient Map:  I made some more liberal cuts, allowing concavity, but thinking about it as if it were a real map. With these two map-creating strategies, I found the total number of pixels on each map and found the total number of green pixels on the map using the GIMP graphics program. 

% interruption = # of green pixels / # of total pixels in the map 

I then divided the two numbers to find the % of the map that was interrupted. The results of this ranking are given in the graph below. 

The least amount of interruption from the Connected Maps was the basketball pieces put into a line, while the basketball flower orientation had the highest % of interruptions. The lowest percentage of disruption for the Efficiency Comparison is the soccer ball, and the highest percentage of interruptions belongs to the efficient cut-up spider.

Figure 6: The image on the left has the least % of interruptions in the connected maps, and the map on the right has the most. 

 

Figure 7: The image on the left has the least % of interruptions in the efficient maps, and the map on the right has the most. 

Figure 8: The more vibrant colors are the efficient versions of the maps, and each different color refers to a different ball(Ex.Beach ball, basketball…)The lower the bar, the less % of interruption and the better the map is.

Results Two: Projections

In this portion of the project, I used Google Sheets and the collected data of where all the cities are on the globe. I wanted to prove that with a single formula, I could transform a 3D sphere into a 2D plane. This worked well, so then, I wanted to see the distortion that the different projections in the form of formulas caused to the map. So, I made a grid out of dots corresponding to the latitudes and longitudes and put them through the same formula transformations. Then, I plotted these dotted grids onto a scatterplot to see the distortions. 

I also thought of a new projection (I haven’t found it anywhere after a quick search). I first took the formula of the central cylindrical projection, which projects the land masses on the globe onto an infinitely upward and downward cylinder.  Realizing that the north and southern poles would never be projected in this projection, I thought the cylinder doesn’t have to be infinite, but with a flat top and bottom. But then, I thought it would be even better if the top and bottom of this new cylinder were another cylindrical projection. This created a cube-type object with curved edges, like a cylinder, rather than flat(See Figure 9).

The math of this proved quite difficult, but finally, I figured that my new blended projection would have an “if” statement (in Google Sheets). So I  added; if long. > 45°, tangent(90°- Long.), otherwards tangent of long to the formula. 

This projection has the following characteristics: the equator and the polar regions have great area and shape conservation. The worst part of the projection is the regions around 45 degrees north or south. 

Figure 9: The two different colored cylinders intersect, and notice how they are equal in size. Imagine a globe in the middle, and then once you unfold the projection, you will get the desired results of my blended projection.

 

Results Three: Lenses

In this portion of the project, I used light bulbs and convex lenses to magnify and flatten a part of a sphere. Unlike the other parts of this project, I am creating an orthographic projection, which only shows almost half of a sphere instead of it all. I will be measuring to see how much difference there is between the edges of my projection and the center.

The refracted image did not change by much in terms of area, though it did change in the shape of the circles. This projection only showed about half of the sphere, but it did it pretty well.

 

Conclusion

In this project, I did three experiments that allowed me to flatten a 3D sphere into a 2D surface. The first experiment was where I cut beach balls in patterns such as soccer or tennis balls. Then, I would find a formula for existing projections and make my versions of those maps, and then a grid with the same formula would be used to show the distortion. Finally, I used a convex lens to project a sphericle lightbulb onto a flat piece of paper, making almost half of the lightbulb visible on the 2D surface.

Balls

I bought seven identical beach balls on which I drew different patterns inspired by sports balls. I then cut out the pattern into flattened pieces and assembled them onto the ground to show a flattened sphere (See Figure 6). The majority of my cutouts were flatter rather than bumpy, while the rest were hard to flatten due to their size; I noticed that the smaller and thinner the pieces were, the flatter they would be. The problem with using this method to flatten a globe is that there are interruptions between the pieces. The smaller the pieces, the more interruptions. If it were an actual globe that I cut, many landmasses would be split in the middle. To determine which “ball map” was best, I used an image manipulation application (GIMP) to count the number of pixels in the background of my cutouts to see how much of the map is interrupted, and the best two “ball maps” are the basketball pieces in a line, and the soccer ball.

Figure 9: Notice that the last image is the assembled flat surface and how it has many interruptions, so I had to pick my poison between more flat or less interruption.

Because of the issue with interruptions, I had cut one of my beach balls like an orange peel with a very thin spiral (See Figure 7), and when placing it on the ground, I tried my best to have no interruptions; it did work, I made two equal circles that where flat and had barely any interruption. But to get to that result, I needed to stretch the spiral to match up “landmasses”(colors on a beach ball), especially at the outer edges of the circles. This means that the area of those landmasses would be stretched instead of being equal area like other cutout patterns.

Figure 10: Notice the two circles. I had to stretch the spiral near the edges, leading to ripping in the plastic.

Projections

I downloaded the coordinates of the longitude and latitude of every city on the globe, and I entered them into Google Sheets. To test the formulas of each projection I had collected in my research, I started by making a simple map projection called the equirectangular projection, where the x-axis is the longitude of a globe, whilst the y-axis is the latitude of a globe. With the same data, I used the formulas of different projections and created a scatter plot, which resulted in different maps with different attributes. I then compared the scatter plots to maps of the same projection, and they matched up nicely.

Now that I could make my own maps, I wanted to see the projection attributes, so I created a grid on Google Sheets and then applied the same formulas to see exactly what each projection looked like (See Figure 11).

Figure 11: Notice that the left image is a distortion map, and the right is an actual map. Also see how on the left, the distance between the lines is equal, but the center dots are farther away than the more northern and southern lines.

Each projection distorted at least one of three things: Shape, Size, or Orientation. Each of the projections I tested, apart from the sinusoidal type, had a good orientation because they all had the north as upwards, south as downward, east rightwards, and west leftwards for all landmasses; whereas, the sinusoidal projection did not have north necessarily up. For the sinusoidal projection, it may not have good orientation, yet it keeps the area of landmasses well conserved. However, this is not the case for many of the other rectangular projections. This analysis shows that a map projection can not hold all three attributes perfectly, but they can be close.

Lenses

Finally, I bought spherical lightbulbs, applied equal-sized circles onto them, and then projected them onto a piece of paper. I projected the pattern via a convex lens, which refracts the image upside down and creates a real image (unlike a concave lens that creates a virtual image). I then took measurements of the circles on the outside of the projected lens and compared them to the inside circles. They turned out to be very similar sizes, which means that the distortion of shape and area is not significant (See Figure 12).

Figure 12: I am drawing the circles throughout the projected image to measure later on and see how the ones on the edges are stretched out.

This experiment was a demonstration of a physical projection, rather than a mathematical formula. This can be also mimicked by taking a photograph of a globe (see figure below). The lightbulb image through the lens and the photograph are both orthographic projections, and they both project only one side of a sphere onto a flat surface.

 

Bibliography

Kuvina Saydaki. (2023, July 29). Map Projections: the Math Behind Every Map [Video]. YouTube. https://www.youtube.com/watch?v=bpp0xCknQAQ

List of map projections. (2025, February 20). In Wikipedia. https://en.wikipedia.org/wiki/List_of_map_projections

Mercator Projection. (2025, March 18). In Wikipedia. https://en.wikipedia.org/wiki/Mercator_projection#Mathematics

Equirectangular Projection. (2024, September 1). In Wikipedia. https://en.wikipedia.org/wiki/Equirectangular_projection 

Sinusoidal Projection. (2024, December 4). In Wikipedia. https://en.wikipedia.org/wiki/Sinusoidal_projection  

Central cylindrical Projection. (2024, November 27). In Wikipedia. https://en.wikipedia.org/wiki/Central_cylindrical_projection 

Gall stereographic Projection. (2024, September 1). In Wikipedia. https://en.wikipedia.org/wiki/Gall_stereographic_projection 

The Geographic Grid. (n.d.). Geography.name. From https://geography.name/the-geographic-grid/

SimpleMaps. (2010-2025). Free world cities database. Retrieved March 18, 2025, from https://simplemaps.com/resources/free-country-cities

 

I aknowledge my mother for helping me find the data of every city in the world and supporting me along the way.